The Problem

In experiments we often capture video and would like to extract information like coordinates to build models. In this article we walk through the process of doing this with a pendulum. Video will be collected via a phone, preprocessed, and then fed to a Python script to extract usable coordinates. Afterwards, the data is fit to a sine curve. Code and output will be found at this link under the folder coord_from_vid.

Processing

After data collection, we need to preprocess the data to make it easier to analyze. In our case, we crop the video, grayscale everything excluding the color yellow, shift yellow to green, and downscale the video to $160 \times 90$. The first steps can be done in Kdenlive or any other video editing software and the last can be done using ffmpeg. The result is shown in out.mp4.

Now it is possible to extract the coordinates. For this project we are interested in extracting the x center of mass coordinate. The code that will perform this operation is contained in process.py.

The idea behind this algorithm is that the only sizable amount of green in each frame is located at the pendulum's position. If it is possible to determine which pixels are green then we simply apply the center of mass formula (assuming constant density) to find the center of mass of the pendulum at any given moment.

Since our video is greyscale in the background and green where the pendulum is, we introduce the following metric between pixels:

$$d(p_1, p_2) = \frac{(r_1-r_2)^2+(g_1-g_2)^2+(b_1-b_2)^2}{3 \cdot 255^2},$$

where each pixel is a $(r, g, b)$ tuple with color values in the range 0 to 255. The denominator in the metric is simply a normalizing factor.

The algorithm can be written quickly. For every frame, scan the image and add the green pixels to the center of mass. Record the center of mass into a file. Repeat for every frame. This algorithm will run into $O(nmK)$ time where $n$ and $m$ and the length and width of the video and $K$ is the number of frames. An optimization will be discussed in the conclusion.

After running the code we get processed data that looks like this. Not too bad!

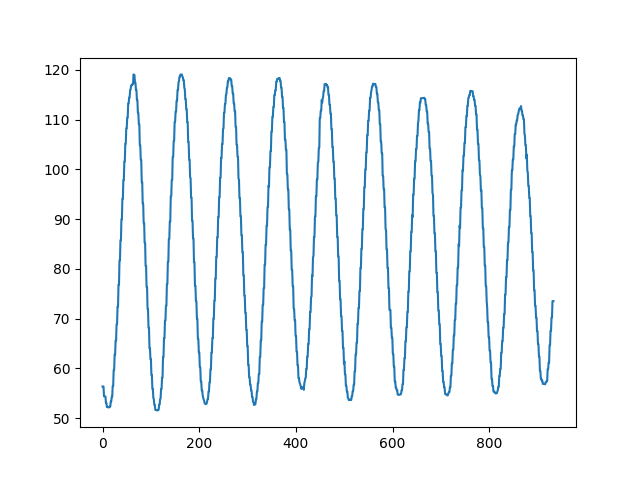
Fitting

To finish we fit a sine model of the form $x(t) = A\sin(Bt+C)+D$ to the data. We estimate the parameters $[A, B, C, D] = [35.0, 3.77, 0.0, 85.0]$ to aid the optimization. We recieve $[A, B, C, D] = [-31.71, 3.77, 0.79, 85.41]$ with standard deviations given by $[0.085, 0.00062, 0.0055, 0.061]$ which are very reasonable. The plot also shows good agreement. Code is found in fit.py.

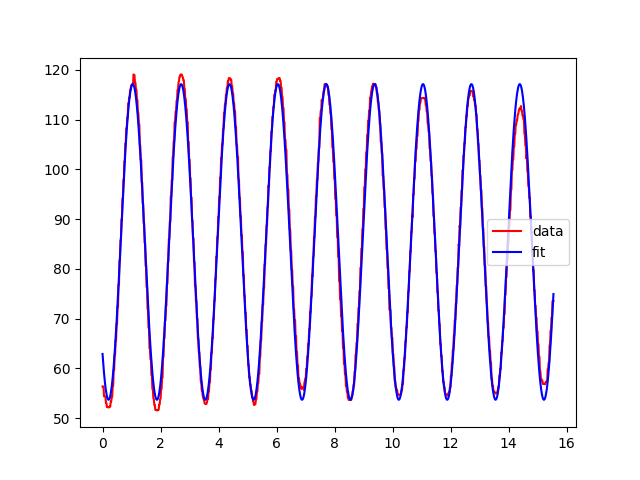
Conclusion

Although things like video analysis seem daunting at first they are actually very manageable. They also have a lot of real life applications in science and engineering.

As mentioned before there is an optimization that did not occur to me until I wrote this article. The idea is that the center of mass moves in a roughly continuous manner so once you know where the blob is at one moment it is easy to calculate the center of mass of the next frame (the low speed of the pendulum and the camera speed ensures this). Given a green pixel, perform a breadth first search to find all other green pixels and record the center of mass. To compute the next center of mass simply start the breadth first search at the last center of mass.

The complexity is a little tricky to analyze. The optimization ensures that the program only goes over pixels in green. This is still technically $O(nmK)$. However, if the blob takes up roughly ten percent the length and width of the frame, then this represents a $100x$ speedup which could make the difference in working with a larger resolution or processing the data in real time.

This is just the starting point for other projects. For example, one could combine this with the algorithm presented in this paper. An ODE model would allow one to go beyond fitting a specific function to learning a model that hopefully generalizes to other conditions. Here is the code and have fun!